Randomization
Randomize to know it is real.
Lesson 1:
Knowing results are real
Summary:
This lesson introduces the problem of confounding variables—variables that influence both the independent and dependent variables in a study. The presence of confounding variables creates challenges for drawing correct conclusions about the relationship between independent and dependent variables. Random allocation is a technique that addresses this problem, by distributing confounding factors across the treatment and control groups. The rest of this unit will teach appropriate methods to implement randomization to support valid conclusions.
Goal:
- Identify how confounding variables can be a problem for drawing the correct conclusions from study outcomes.
- Examine the data to identify potential confounding variables.
- Recognize how random allocation supports rigor by distributing confounding variables across treatment and control groups.
Example study: lithium vs. control in ALS mouse model
To understand the role of randomization in experimental design, let's examine a neuroscience study. A team of researchers is investigating whether lithium treatment could improve survival in an ALS mouse model based on previous findings from Fornai et al. 2008. They're working with SOD1-G93A mice, a transgenic mouse model of ALS, between 60-90 days old, comparing the effects of lithium carbonate solution against a saline vehicle control. To measure the treatment's effectiveness, they'll track survival time after treatment initiation. Before treatment, researchers recorded mouse characteristics including age, sex, weight, and disease stage (time on rotarod).
Balancing controls vs. lithium treatments
The research team develops a protocol to balance how many mice are treated vs. controls. When selecting mice for treatment groups, they work cage by cage. From each cage of four mice, they first catch two mice which receive the vehicle control (saline solution). The remaining two mice in the cage are then assigned to receive the lithium treatment.
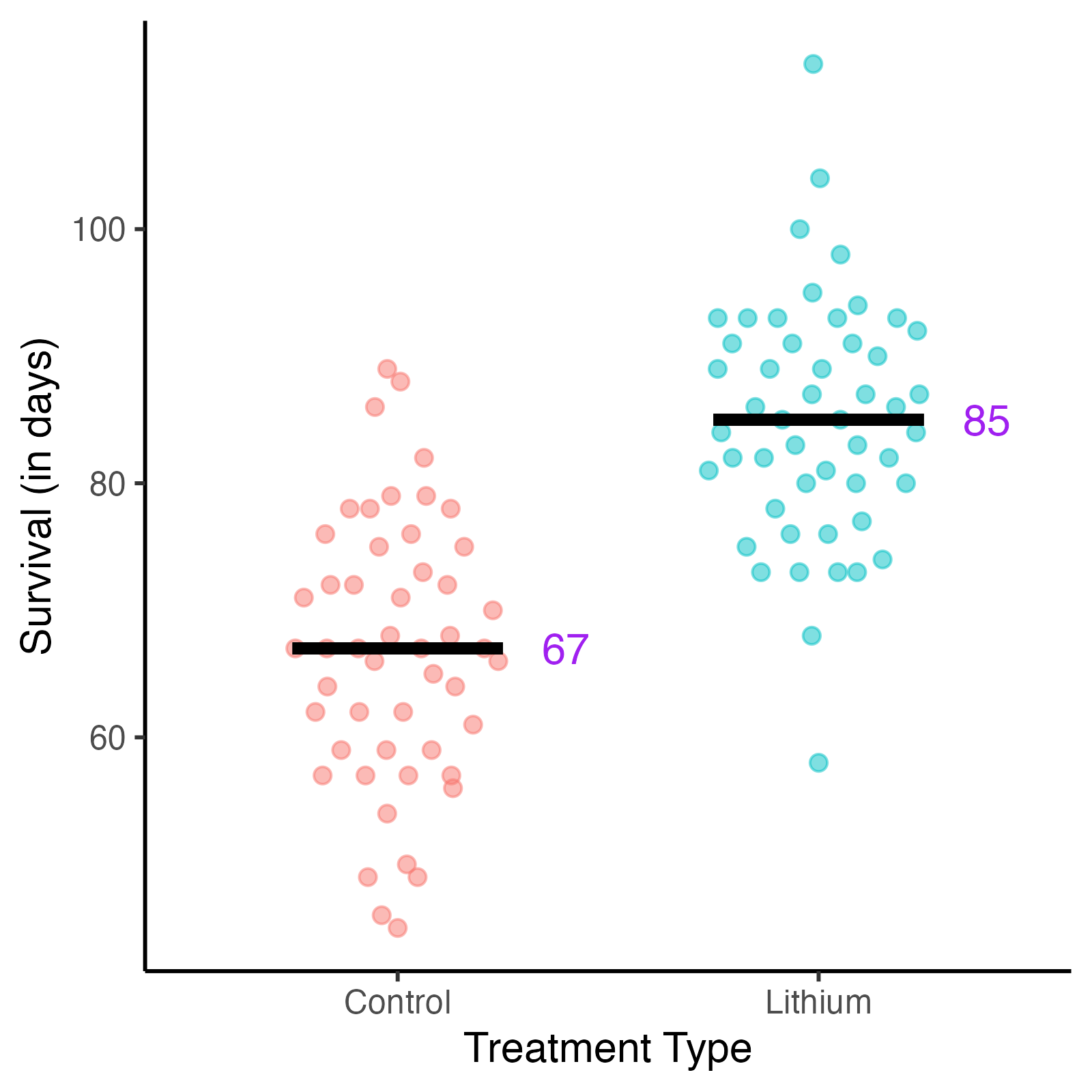
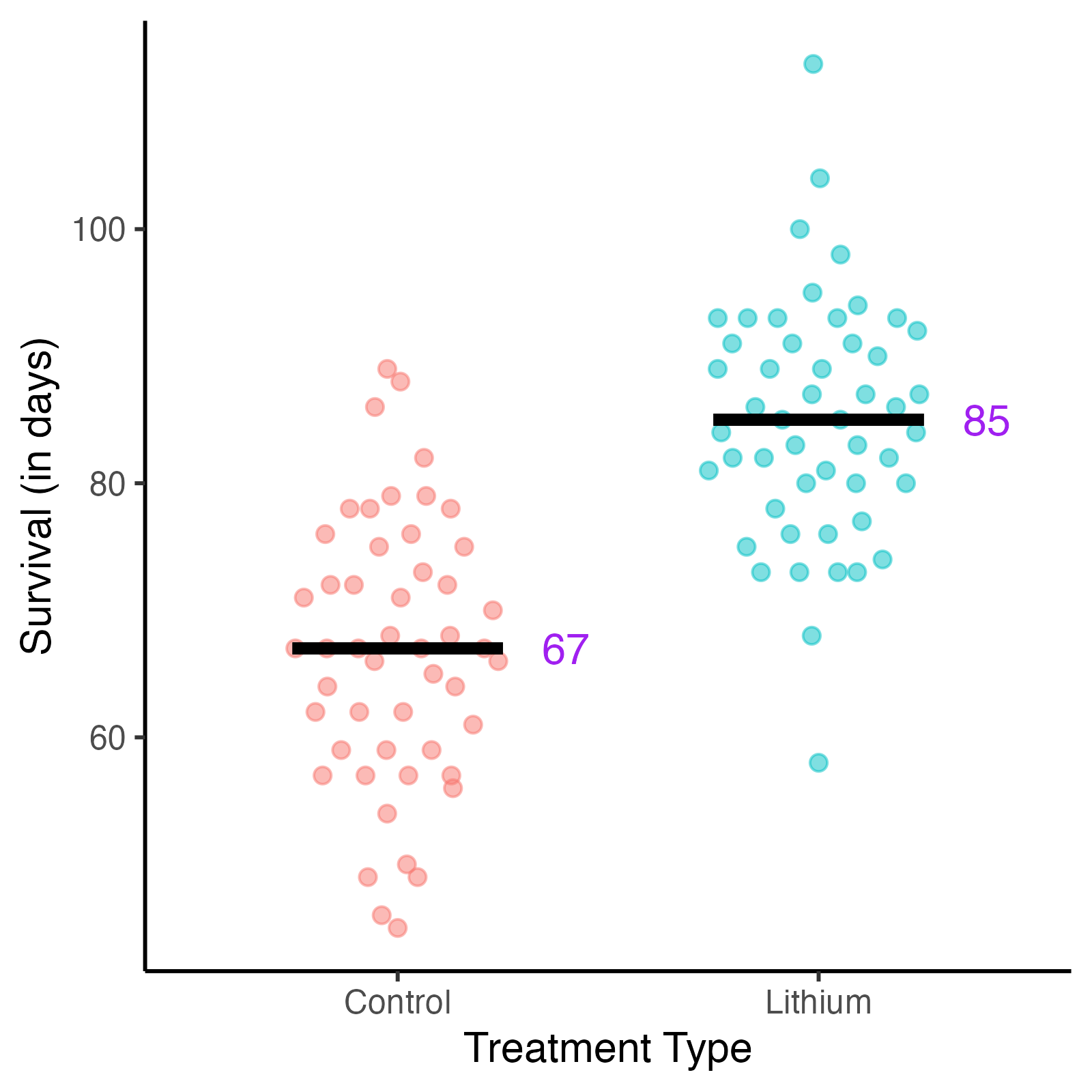
Did lithium slow ALS disease progression?
After running the experiment and analyzing their data, they find encouraging results. The mice in the lithium treatment group show longer survival times compared to the control group, and the treatment effect appears promising. Based on these initial findings, it seems lithium could potentially improve outcomes for ALS patients.
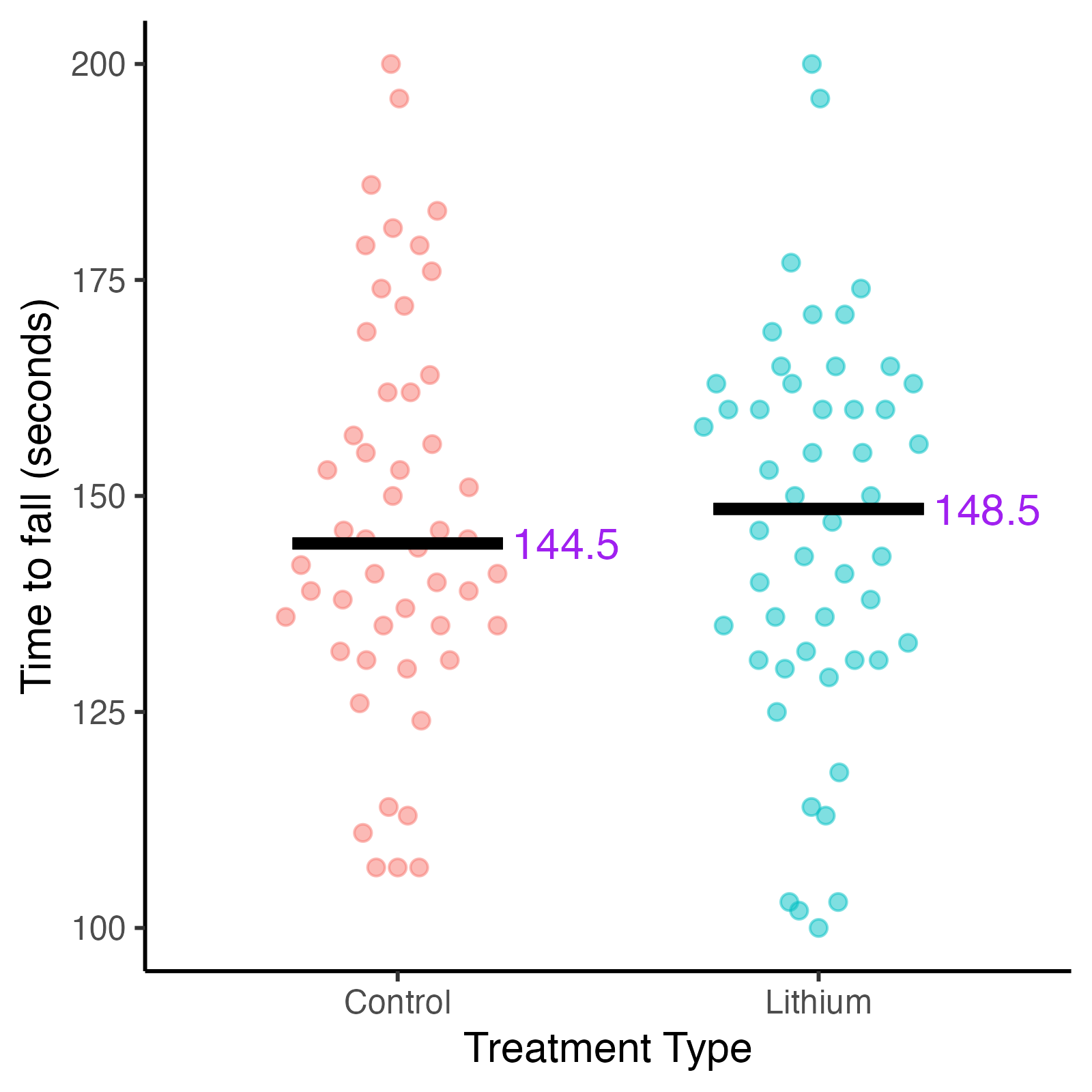
Fig. 2. Survival vs treatment type in mice.
Survival in days following treatment with lithium solution or saline solution (control).
Examining the evidence
However, before accepting these results, let’s carefully examine their experimental design and data. Several questions emerge: What exactly is driving the survival difference between these groups? Can we confidently attribute this effect to the lithium treatment? We need to consider what other factors might influence both how mice were assigned to treatment groups and their survival. How can we validate these conclusions?
Let’s look at several mouse variables that could affect these results: weight, sex, which litter they came from, and age. We need to also look at the mice's disease stage. In this model, a rotarod test is used to monitor the disease progression. As motor neurons die and muscles waste, the mice fall off the rotarod sooner. Thus, decreased “time to fall” may indicate more advanced disease stages. Which of these factors might have influenced the treatment assignment or survival of the mice?
Activity #1: How do I know it is real?
Analyze one variable to identify potential relationships with treatment assignment and survival.
Post-activity questions:
- Which covariates are a problem for drawing a conclusion about lithium treatment?
- Besides the confounders that were provided, are there others that could be relevant?
A closer look at mouse behavior
Our analysis of the experimental procedure reveals a pattern in how mice were selected for different treatment groups. The researchers notice that more active mice are consistently harder to catch, while less active mice are typically caught first. In this ALS mouse model, activity level correlates with disease progression. Mice in earlier disease stages are more active, while those in later stages show reduced activity (Knippenberg et al. 2010).
Disease progression influences treatment
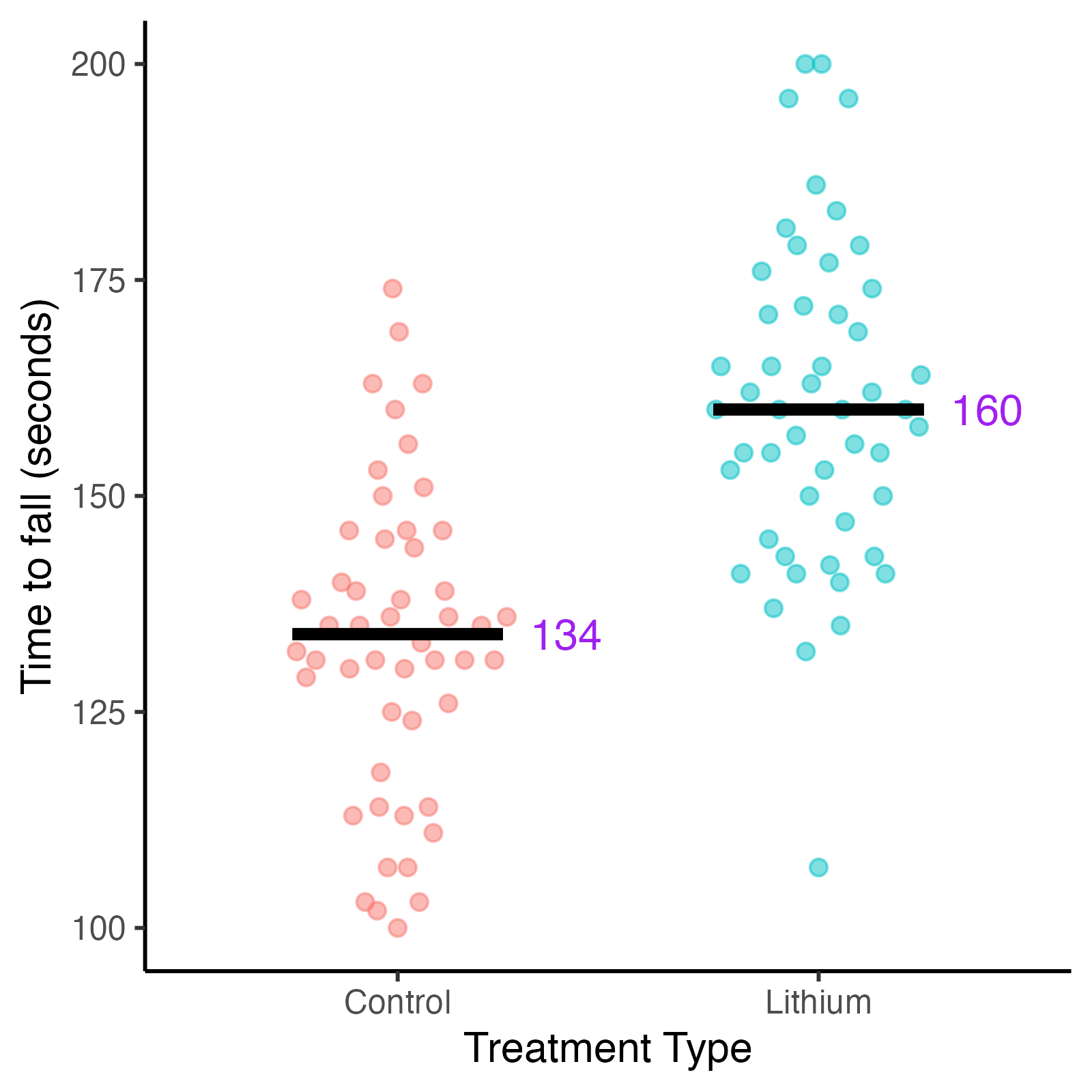
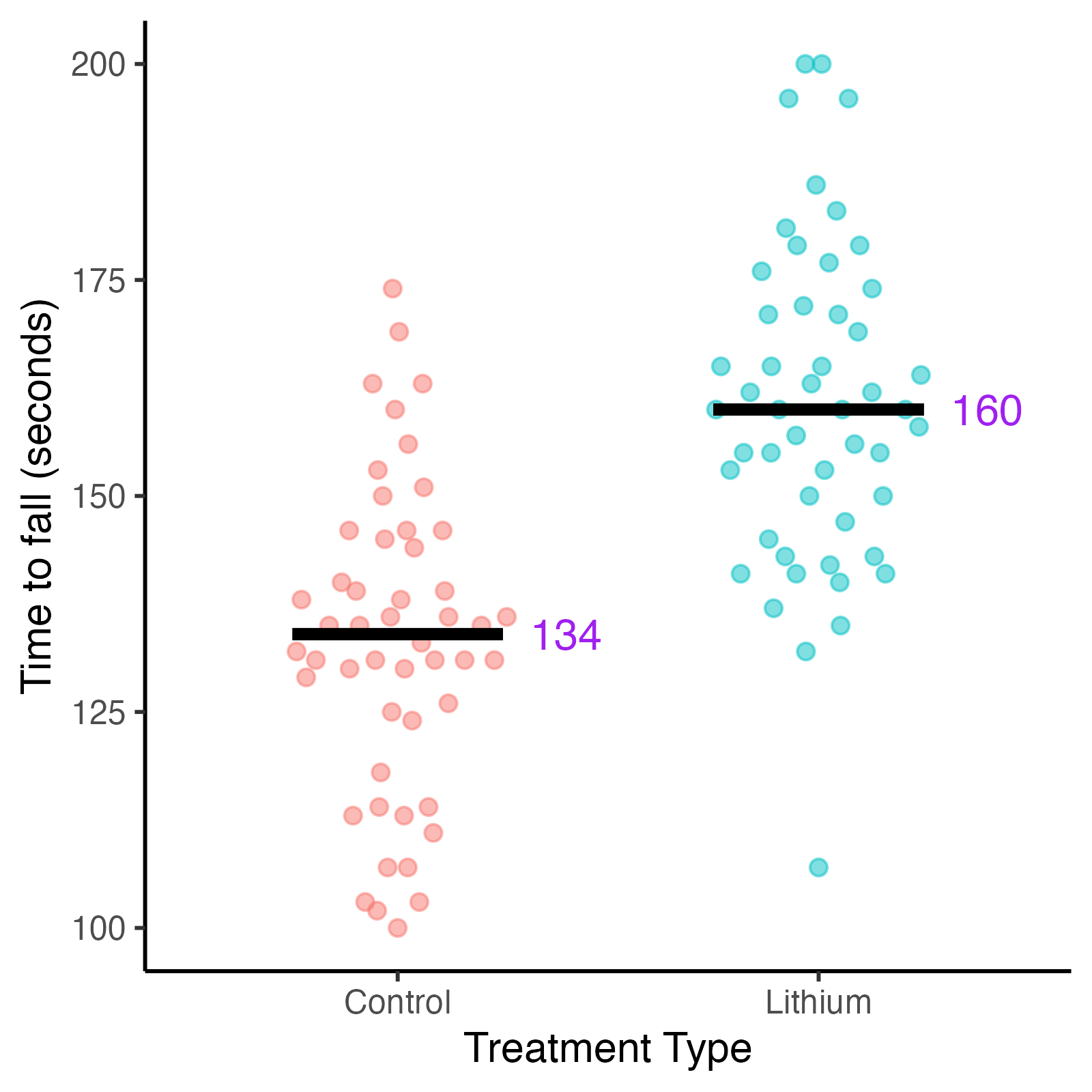
Examination of the data confirms a disease progression bias in treatment selection. The mice that ended up in the lithium treatment group were predominantly in earlier disease stages, meaning they had longer times holding the rotarod (time to fall). The control group contained more mice in later disease stages.
Fig. 3. Distribution of time to fall in seconds for mice by treatment type.
Disease stage is measured by the time a mouse remains on rotarod (time to fall), measured in seconds. Shorter times equal advanced disease stage.
Disease progression relates to survival rates
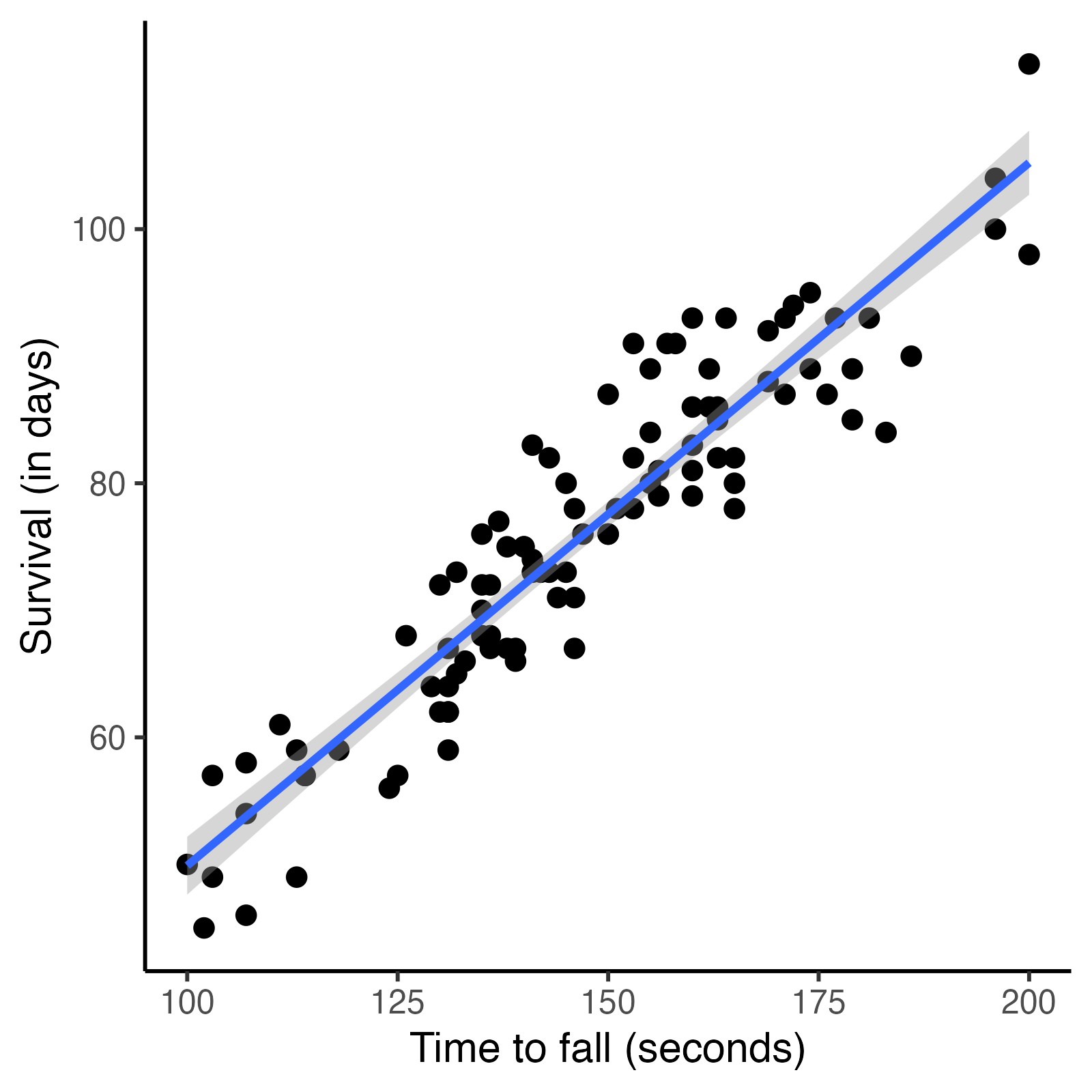
Disease stage is related to survival - mice in earlier disease stages survive longer.
Fig. 4. Survival vs time to fall in mice.
Disease stage is measured by the time a mouse remains on rotarod (time to fall), measured in seconds. Shorter times equal advanced baseline disease stage.
The problem of confounding
A confounding variable is a variable that influences both independent and dependent variables in a study. They create an indirect dependency between independent and dependent variables. As a result, confounding variables can mask or amplify the influence of an independent variable on a dependent variable.
In this study, the relationship between disease stage, group assignment, and survival illustrates makes disease stage a confounding variable.
Disease stage creates a spurious correlation between treatment and survival that complicates our interpretation of the results. A characteristic of the mice - specifically their disease stage - influenced both whether they were assigned to receive lithium treatment and how long they survived. This creates ambiguity about the treatment effect: are we seeing longer survival because of the lithium, or simply because the lithium group happened to include more mice in earlier disease stages?
Implications for this study: we don’t know it is real
The implications of this confounding extend beyond just disease stage. While we've identified disease stage as a confounder, there might be other confounding variables that they did not measure. Even more concerning, there could be confounding variables they don't even know about and therefore couldn't measure. This kind of systematic bias in treatment assignment makes it impossible to draw clear conclusions about the treatment's effectiveness.
The power of proper randomization
If this study had used proper randomized allocation of treatment assignment from the start, the distribution of mice at different disease stages would have been distributed evenly between the treatment groups (Kang et al. 2008). Rather than disease stage being systematically related to treatment assignment, randomization would have allocated mice of all disease stages between the lithium and control groups.
Fig. 5. Non-randomized treatment allocation vs. randomized treatment allocation.
a. Distribution of disease stage of mice by treatment group, not randomized.
Fig. 5. Non-randomized treatment allocation vs. randomized treatment allocation.
b. Distribution of disease stage of mice by treatment group, randomized.
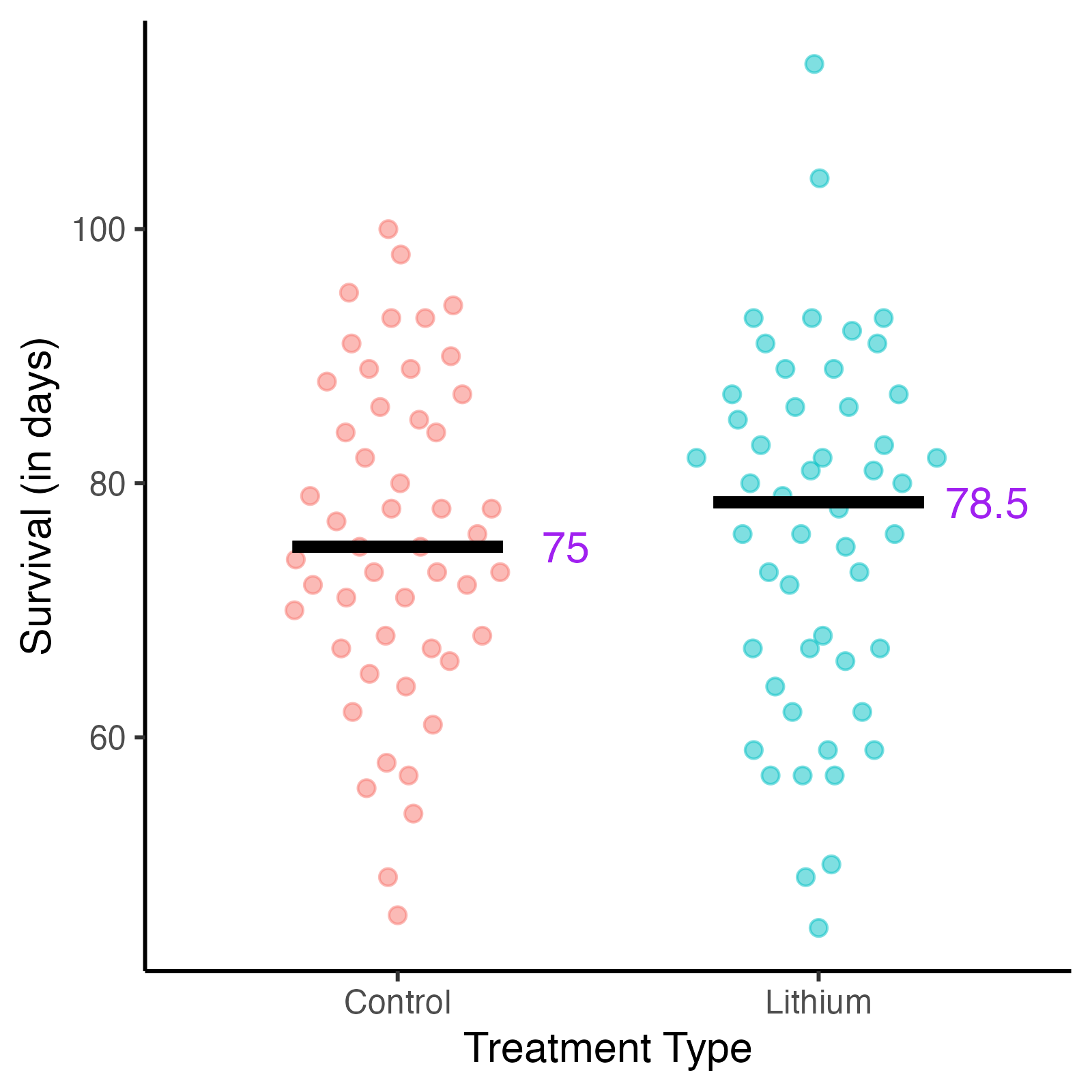
Random allocation reduces the risk of bias
When we randomize treatment assignments, we distribute potential confounding factors - both the ones we know about and the ones we don't. Randomizing which mice receive lithium vs. control will allow the researchers to study the relationship between lithium treatment and survival, and to make valid causal inferences about the treatment's effectiveness.
Fig. 6. Non-randomized treatment allocation vs. randomized treatment allocation.
a. Survival of mice by treatment group, not randomized.
Fig. 6. Non-randomized treatment allocation vs. randomized treatment allocation.
b. Survival of mice by treatment group, randomized.
Next time, randomize!
What if these researchers revised their experimental approach? Instead of assigning treatments based on which mice are caught first, they implement randomization of treatments from the very beginning. Before any handling begins, each mouse should be randomly assigned to either the lithium or control group. This ensures that the ease of catching a mouse has no relationship to which treatment it receives.
Random allocation provides multiple benefits for experimental design. It reduces biases in how samples are assigned to treatment groups. Randomization can help avoid unbalanced groups where one treatment has significantly more subjects than another. Perhaps most importantly, it distributes the effects of both known and unknown confounding variables across treatment groups. This distribution allows us to make stronger causal inferences about treatment and ensures we meet the assumptions required for statistical tests.
Practical implementation
To implement proper randomization in this ALS study, they need to make several specific changes to their protocol. Before beginning any experimental procedures, they must generate a complete randomization sequence that assigns treatments to all mice. This sequence should be created using appropriate randomization software or methods, not by arbitrary selection. They must strictly follow this pre-generated sequence when providing treatments, regardless of how easy or difficult each mouse is to handle. In later lessons, we will talk through the details of how to implement this randomized sequence into different research scenarios, and how to ensure that the appropriate people are kept masked from which mice are receiving which treatment. Throughout the experiment, they must carefully document the randomization process and any deviations that occur.
By following these more rigorous procedures, the researchers can be much more confident in their conclusions about whether lithium truly affects disease progression in this ALS model. The extra effort required for proper randomization is outweighed by the increased validity and reliability of results.
Takeaways:
- Without proper randomization, confounding variables (like disease stage in the ALS mouse example) can create misleading correlations between treatment and outcomes, making it impossible to determine if observed effects are truly caused by the intervention.
- Random allocation of subjects to treatment groups distributes both known and unknown confounding factors across groups, allowing researchers to make valid causal inferences about treatment effectiveness.
- Implementing a complete randomization sequence before beginning an experiment and strictly following it throughout the study is essential for reducing systematic bias and increasing the validity and reliability of research findings.
Reflection:
- What are the kinds of confounding variables that are most relevant to your research?
- What challenges do you imagine could arise when implementing randomization protocols?
- How would you explain to a non-scientist, the importance of randomization for ensuring proper conclusions?
Lesson 2:
Randomization in the wild: avoiding common mistakes
Summary:
This lesson explores what it means to have a random allocation sequence. Why is alternating allocation between treatment group and control group an issue? It turns out that non-random allocation can introduce systematic biases that are a problem for producing rigorous results. Although true random allocation may appear unbalanced, it achieves the primary goal of implementing random allocation: eliminating systematic biases to produce valid conclusions.
Goal:
- Distinguish between random allocation sequences and other allocation sequences that are balanced.
- Recognize how non-random allocation sequences can introduce bias that challenge study validity.
- Recall that the primary goal of random allocation is to reduce systematic biases.
A need for balance
In Lesson 1, we explored how the lithium treatment study was compromised when researchers unknowingly assigned mice to treatment groups based on how easy they were to catch. Imbalanced group characteristics led to confounding, where differences in outcomes (survival) were caused by pre-existing differences between groups (disease stage) rather than the intervention itself (lithium). This cautionary tale illustrates a fundamental rigor principle: if your treatment and control groups aren’t comparable at baseline, you cannot confidently attribute any differences in outcomes to your intervention.
Therefore, when designing experiments, researchers face two fundamental balancing challenges:
- Balance in group characteristics: Creating treatment groups that are comparable in all aspects except the intervention being tested. This balance is needed for drawing valid conclusions about whether your treatment actually caused the outcome. Many statistical tests we rely on assume that observations are independent and groups are equivalent at baseline. When these assumptions are violated, the interpretation of our results must take these violations into account.
- Balance in group sizes: Ensuring that treatment groups have similar numbers of samples (equal Ns), which gives you the most statistical power to detect real effects.
If one group has far fewer samples than another group, the precision of estimates for the group with fewer subjects decreases, potentially obscuring real treatment effects or requiring larger overall sample sizes to achieve the same power. With uneven group sizes, your ability to detect real effects decreases, and you might miss important discoveries.
What if you want to balance treatment groups in a study - how would you do it?
Balancing treatment groups in the wild
Researchers often recognize these needs for balance and try various approaches to achieve it. Let’s look at some common methods:
- A parasitologist inoculates a treatment mouse with parasites, immediately followed by a control mouse, repeating for subsequent pairs of mice
- A cell biologist evaluates a control cell first, followed by the most similar treatment cell, repeating this pattern of matched evaluation for every cell
- A clinician assigns the patients in the first week of an epidemic wave to receive treatment, and the next week to control
- A neuroscientist assigns treatment equally by tank in their lab, where fish numbers are equal per tank
- A research assistant manually assigns participants to "balance things out" based on their judgment
- A clinical trial coordinator assigns treatment group based on patient’s date of birth or date of trial entry
- A surgeon conducts the sham surgeries in the morning and an equal number of experimental surgeries in the afternoon
These approaches may seem reasonable and can create the appearance of balance, but they can introduce biases. Unfortunately, such approaches are often reported as “randomized” in the literature. Let’s see if we can identify the differences between truly random assignment and these other approaches.
Activity #2: The challenge of true randomization
When researchers claim to use randomization in their studies, what does that actually mean in practice? In this activity, consider three sequences from published studies that all claimed to use "randomized allocation".
Which one represents true randomization? For this activity, we display the group sizes (number of samples in treatment A vs. treatment B), effect sizes (measure of the strength of the phenomenon being studied), and p-values (measure of statistical significance).
Post-activity questions:
- What properties did you use to decide whether a sequence was random?
The deceptive nature of alternation: the problem with Sequence 1
Looking at Sequence 1, we see a perfect alternating pattern between treatments A and B. For example, our parasitologist above who inoculates a treatment mouse with parasites, immediately followed by a control mouse. This creates perfectly equal group sizes, but it introduces several potential biases:
- Selection bias: If researchers know the next assignment will be treatment B, they might unconsciously select a "better" participant for that group. Imagine a researcher thinking "the next animal looks stressed” and making a judgement call about whether to enroll them into a stressful intervention or moving to the next animal instead.
- Performance bias: Predictable treatment assignments can affect how researchers interact with samples. If you know a mouse is in the control group, might you unconsciously handle it differently than if it were in the treatment group? Small changes can create systematic differences in care that are unrelated to the treatment itself.
- Temporal confounding: Environmental factors that vary systematically with time (morning vs. afternoon, day of week, seasonal effects) become confounded with treatment groups. This can include personnel effects if certain staff are more likely to work with one treatment group due to work scheduling. It can also include any changes that can happen over time: desiccation of a cell, wearing down of an instrument, or even the improvement in treatment skills over time.
Consider a study where treatment A (control) is always administered to a zebrafish in the morning and treatment B in the afternoon due to this alternating pattern. Any natural variations in zebrafish physiology related to light or temperature would become entangled with the treatment effect. Additionally, the researcher might unconsciously select healthier-looking fish for a certain treatment or handle the fish differently based on the predictability of the treatment assignment.
Human attempts at "randomness": the problem with Sequence 2
Sequence 2 might feel more “random” at first glance. It avoids patterns while maintaining balance between treatments. However, this sequence shows signs of manual allocation by a researcher attempting to "look random."
When humans try to generate random sequences manually, we have “tells” that make it easy to distinguish our sequences from real random sequences:
- We avoid long runs of the same value, rarely putting more than 2-3 As or Bs in a row
- We maintain closer to 50-50 balance than true randomness would produce
- We create patterns that "feel" random to us, but aren’t actually random
Manual allocation looks more “random" than alternating allocation, but it comes with the same risk of bias. A researcher might think, "We've had several sicker-looking animals in group B, so I'll put the next healthy-looking one there to balance things out." selection bias happens unconsciously and we cannot trust our intuition as to whether our treatment assignments feel “random enough”. Learn more about the impact of unconscious bias in research in our Confirmation Bias Unit.
True randomization revealed: why Sequence 3 is different
Sequence 3 might have seemed less "random" than Sequence 2, but it is the only randomized sequence! True randomization often produces results that surprise us:
- It can create long runs of the same value (like seven A's in a row)
- It may result in unequal group sizes (here, 20 A's and 10 B's)
- It doesn’t feel random! Human brains are pattern-seeking, and true randomness often feels wrong to us. We might notice how any random sequences in a row might start with A, or we think we see patterns or tendencies that feel non-random
Our intuitions about randomness can lead us to try other methods instead, but true randomization is key for containing bias in research. Compared to these other approaches, only randomization:
- Reduces selection and performance bias in research
- Ensures independence of assignments
- Allows valid statistical inference
- Balances both known and unknown confounding variables
With alternating allocation, temporal effects get amplified across hundreds of samples. If morning vs. afternoon creates even a small physiological difference in your samples, this effect compounds across the entire study, potentially creating a false treatment effect.
Manual allocation gives unconscious biases more opportunities to create systematic differences between groups. Even small biases in how researchers assign treatments can accumulate into significant group differences.
In contrast, while true randomization might create some imbalance in smaller samples, it tends to produce more comparable groups overall. The larger the study, the more likely that important variables will be distributed similarly between groups.
When “random” isn’t actually random
Sometimes, methods that appear random actually follow predictable patterns or systematic rules. You can distinguish this false randomization from true randomization if the allocation techniques can be reproduced to yield identical group assignments repeatedly. Common examples include assigning treatments based on odd or even identification numbers, using sample birth dates or admission dates, or allocating treatments by position in plates, cages, or tanks.
False randomization can even occur when researchers start with proper randomization methods. Bias can infiltrate during implementation if researchers generate a proper random sequence but then selectively apply it, regenerate "unfavorable" sequences until getting one that looks better, or make post-hoc adjustments to achieve what feels like “better” balance.
To maintain the integrity of the randomization, sample selection should occur independently of group assignment. For instance, group allocation assignments can be done in advance using animal/sample identification numbers. If a researcher first consults the random sequence and then selects a sample to allocate into the designated group, they might inadvertently introduce bias when implementing randomization. They might think, "I got a 'B' assignment, let me choose this particular mouse for the B group." This subtle procedural detail makes a significant difference in maintaining the integrity of randomization by ensuring that sample selection happens independently of treatment assignment, preserving the core benefit of randomization—the elimination of systematic biases that could affect experimental outcomes.
Instead, researchers should ensure their randomization method is stochastic and not reproducible. Researchers should use random number generators, generate complete randomization sequences before beginning studies, conceal these sequences from personnel involved in recruitment and treatment, and strictly follow the pre-specified sequences without deviation.
Real-world consequences of non-random allocation
Remember those other balancing approaches mentioned in the beginning of this lesson? Let’s take a deeper look at how those choices impacted their studies:
Parasite buildup: In the parasitology study where researchers alternated mouse assignments, parasites built up in the dropper between the first dose and the second dose because the parasites were clumping to the sides. This meant that the second mouse always received more parasites. With treatment mice consistently assigned and treated first, the control group systematically received higher parasite loads, confounding the results.
Cell desiccation: In the cell experiment where controls were always processed first, the treatment cells experienced longer exposure to air and slightly more desiccation. This made the order of cell processing a confounding variable affecting cell viability independently of the treatment.
Epidemic virulence: When clinicians assigned the first week of patients in an epidemic to treatment and the next week to control, they inadvertently created a temporal confound. As epidemics progress, pathogens often evolve reduced virulence, meaning control patients (who came later) had less virulent infections.
Skill improvement: In the surgical intervention study, the first patients of each day received the surgical sham procedure while later patients received the experimental procedure. Over the day, surgeons improved their technique, creating an advantage for the later patients that had nothing to do with the intervention itself.
Environmental gradients: In the zebrafish study, researchers assigned treatments "randomly" by tank position. However, undetected temperature and light gradients across the room created systematic environmental differences between treatment groups, violating the statistical assumption of independence.
Remember the goal
The goal of randomization isn't to create perfectly balanced groups or sequences that look random to our eyes. Instead, randomization serves to eliminate systematic biases, eliminate non-systematic unconscious bias, and allow valid causal inference about treatment effects. In the above scenarios of the consequences of non-random allocation, the lesson is not that we need to identify every source of bias. Instead, we cannot know and anticipate all confounding variables, so randomization helps minimize the risk of known and unknown confounds.
In the next lesson, we'll explore different methods of randomization and how to select the best approach for your specific research context.
Takeaways:
- True randomization often produces results that appear non-intuitive (like long runs of the same treatment or unequal group sizes), yet it remains essential for reducing selection and performance bias while distributing both known and unknown confounding variables across treatment groups.
- Common non-random allocation methods like alternation, manual allocation, or assignment based on characteristics may create the appearance of balance but introduce systematic biases that can invalidate research findings.
- To maintain randomization integrity, researchers should use proper random number methods, create complete randomization sequences before beginning studies, conceal these sequences from personnel involved in recruitment and treatment, and follow pre-specified sequences without deviation.
Reflection:
- What are some simple ways you can implement random allocation in the lab to reduce the temptation to use haphazard or alternating allocation?
- What are other examples of time-related factors that could be a problem when using an alternating allocation sequence?
- How would you convince a colleague that an "unbalanced-looking" random allocation is actually more desirable than a balanced allocation sequence?